「全ての三角形は二等辺三角形である」
こんなことを書くと、「そんな馬鹿な」と思われてしまうだろう。
勿論、全ての三角形が二等辺三角形だなんて馬鹿なことはある筈が無い。
しかし乍ら、世の中には「全ての三角形は二等辺三角形である」とする「証明」が存在するのである。
「証明」自体は大して難しくはない。
中学校程度の論証でできてしまう。
勿論この証明にはウソが含まれる訳であるが、あなたはこの「ウソ」を見破ることができるだろうか？
念のため言っておきますが、以下の「証明」は「ウソ」です。
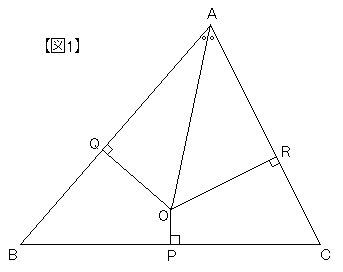
△ABC は任意の三角形とする。
∠A の二等分線と辺 BC の垂直二等分線の交点を O とし、点 O から辺 BC, AB, AC に下ろした垂線の足をそれぞれ P, Q, R とする。《図1》
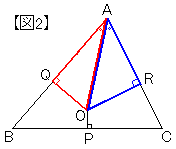
△OAQ と △OAR について、
• OA は共通
• ∠OAQ = ∠OAR （OA は ∠A の二等分線）
• ∠OQA = ∠ORA = 90°
直角三角形の斜辺と1鋭角がそれぞれ等しいので、△OAQ ≡ △OAR 《図2》
∴ AQ = AR …①, OQ = OR …②
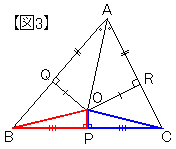
△OBP と △OCP について、
• OP は共通
• BP = CP （P は辺 BC の中点）
• ∠OPB = ∠OPC = 90°
2辺とその夾角がそれぞれ等しいので、△OBP ≡ △OCP 《図3》
∴ OB = OC …③
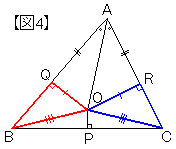
△OQB と △ORC について、
• OQ = OR （②より）
• OB = OC （③より）
• ∠OQB = ∠ORC = 90°
直角三角形の斜辺と他の1辺がそれぞれ等しいので、△OQB ≡ △ORC 《図4》
∴ QB = RC …④
①と④より AB = AQ + QB = AR + RC = AC
∴ △ABC は AB = AC の二等辺三角形 ■
解説を書いたが、できるだけ見ないで自分で考えてみて欲しい。