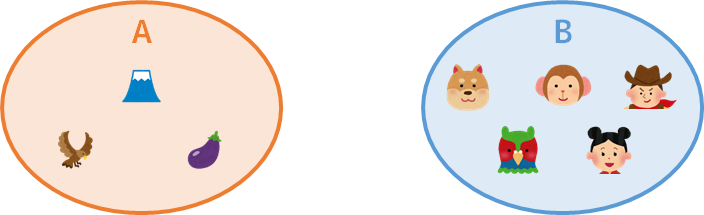
例として、下図の集合 A と B とについて、どちらが要素の個数が多いかを比較する。[注1]
(見るからに B の方が多いのだが、あくまで例として割り切ってほしい)
この記事で言う「個数」とは、集合論で言う「濃度」を指します。
ご存知の通り、「偶数」とは2の倍数のことを指す。すなわち、次のような数である。 …, −14, −12, −10, −8, −6, −4, −2, 0, +2, +4, +6, +8, +10, +12, +14, … 一方、「奇数」とは2で割り切れない整数のことを指す。すなわち、次のような数である。 …, −15, −13, −11, −9, −7, −5, −3, −1, +1, +3, +5, +7, +9, +11, +13, +15, … 偶数と奇数の個数が同じであることは、然程直観に反しないだろう。
では、有理数はどうだろうか?
「有理数」とは、整数同士の分数で表せる数である。すなわち、次のような数である。
0, ±1, ±2, ±3, …;
±12,
±22,
±32, …;
±13,
±23,
±33, …;
±14,
±24,
±34, …; …
見ての通り、「有理数」は偶数や奇数はおろか、整数以外の様々な分数をも含んでいる。
すると一見偶数や奇数よりも有理数の方が圧倒的に多そうである。
だが、実際には「偶数と有理数の個数は同じ」なのである。
一体どういうことだろうか?
偶数も有理数も無限個存在するので、個数を数え上げて比較することはできない。
では、どうやって比較するのだろうか?
無限個の場合を考える前に、まずは有限個の場合の個数の比較方法を考える。
例として、下図の集合 A と B とについて、どちらが要素の個数が多いかを比較する。[注1]
(見るからに B の方が多いのだが、あくまで例として割り切ってほしい)

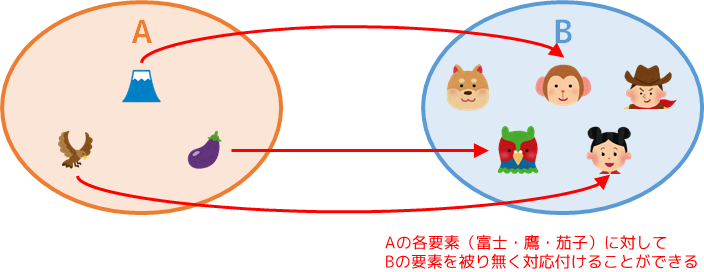
まず、集合 A の1つ1つの要素に対し、被らないように集合 B の要素を対応付ける。
すると、下図の矢印で示すように、集合 A の各要素について対応する B の要素を定めることができる。(対応付けはこの通りでなくても構わない)
このように被りの無い対応付けが可能なとき、「A の個数 ≦ B の個数」であると言える。
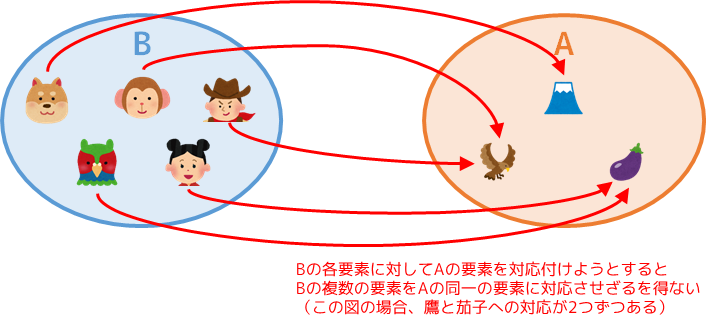
一方、今度は集合 B の1つ1つの要素に対し、集合 A の要素を対応付けようとしてみる。
すると、どのように対応付けたとしても、下図の矢印で示すように集合 A の要素が必ず被ってしまう。
このように被りの無い対応付けが不可能なとき、「B の個数 ≦ A の個数」ではないと言える。
以上より、「A の個数 ≦ B の個数」であるが「B の個数 ≦ A の個数」ではないということがわかった。
これはすなわち「A の個数 < B の個数」であるということである。
このように、被りの無い対応付けが可能であるか否かを考えることで、個数が無限個になった場合でも、2つの個数の大小を比べることができる。
今度は、下図の集合 A と C とについて、どちらが要素の個数が多いかを比較する。
上の例と同様に対応付けを考えると、次のようになる。
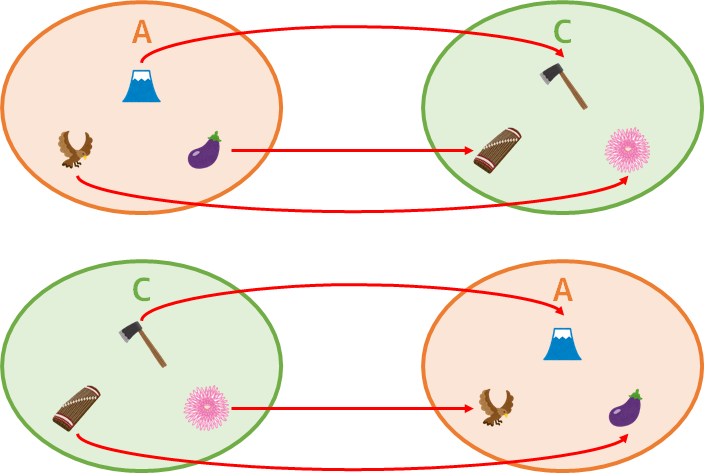 この例の場合、A から C へも、また C から A へも、いずれも被り無く要素を対応付けることができる。
この例の場合、A から C へも、また C から A へも、いずれも被り無く要素を対応付けることができる。
このとき、下図のように A の各要素と C の各要素とを一対一に対応付けることができる。(ベルンシュタインの定理)
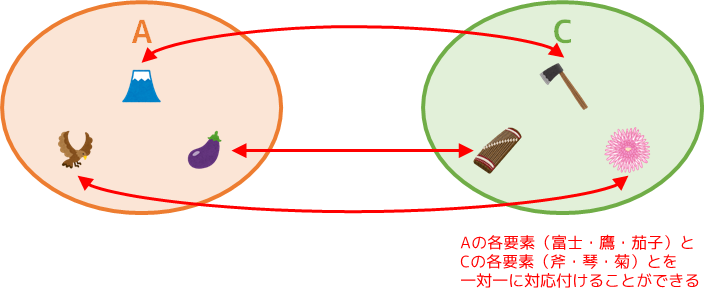 このような一対一の対応付けが可能な時、「A の個数 = C の個数」であると言える。
このような一対一の対応付けが可能な時、「A の個数 = C の個数」であると言える。
冒頭の命題「偶数と有理数の個数は同じ」に戻る。
いきなり偶数と有理数の対応付けをしてもよいのだが、まずはより簡単な偶数と自然数との対応付けを考える。
ここで、「自然数」とは次のような数である。(本稿では 0 も自然数に含めるものとする)[注2]
自然数と他の集合 X との対応付けを行うには、まず X の要素を「最初の数」「次の数」「その次の数」… といった具合に一方向に並べなければならない。(下図)
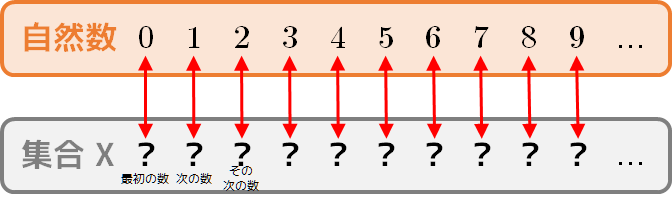
ここで、正の偶数と負の偶数とを次のように交互に並べてみる。
0, −2, +2, −4, +4, −6, +6, −8, +8, −10, +10, …
このようにすることで、全ての偶数を一方向に並べることができる。
すると、下図のように自然数と偶数との間に一対一の対応付けができる。
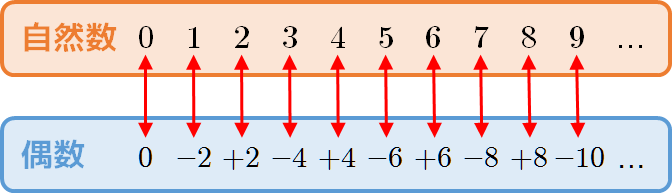
これはすなわち、「偶数と自然数の個数は同じ」ということを意味する。
今度は有理数と自然数との対応付けを考える。
簡単のため、0 や負の数は一先ず置いておいて、まずは正の有理数のみを考える。
有理数を自然数と対応付けるためには、偶数のときと同様に、有理数を一方向に並べなければならない。
とは言え、有理数(分数)には分子と分母とがあり、一筋縄では並べられない。(下図)
では、どのようにすれば並べられるのだろうか?
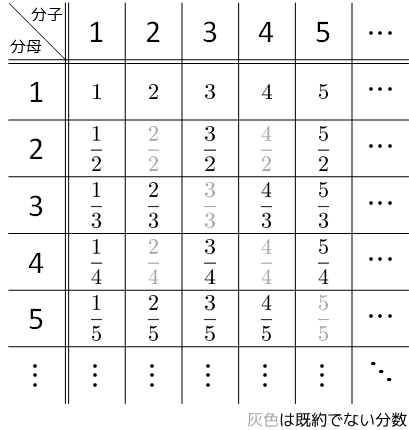
答えは下図の矢印の通りである。
表を斜めに見ていけば、有理数を並べることができる。

上図の矢印の通りに有理数を並べると次のようになる。(既約でない分数は除外)
1, 2, 12, 3, 13, 4, 32, 23, 14, 5, 15, 6, 52, 43, 34, 25, 16, 7, 53, 35, 17, 8, …ここに 0 や負の数も加えると、次のようになる。
0, −1, +1, −2, +2, − 12, + 12, −3, +3, − 13, + 13, −4, +4, − 32, + 32, − 23, + 23, …
斯くして全ての有理数を一方向に並べることができた。
よって、下図のように自然数と有理数との間に一対一の対応付けができる。
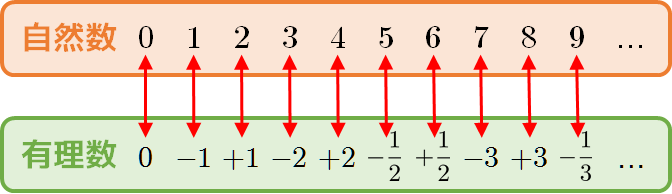 これはすなわち、「有理数と自然数の個数は同じ」ということを意味する。
これはすなわち、「有理数と自然数の個数は同じ」ということを意味する。
「偶数と自然数の個数は同じ」であり、かつ「有理数と自然数の個数は同じ」であるから、結局「偶数と有理数の個数は同じ」であると言える。
同じ理屈で、自然数・素数・偶数・奇数・整数・有理数等は全て同じ個数であると言うことができる。
この個数のことを「可算無限濃度」と呼び、「ℵ0」(アレフ・ゼロ)と表す。
因みに、無理数や実数の個数は偶数や有理数とは異なり、もっと多い。(カントールの定理)
無理数や実数の個数は「連続体濃度」と呼び、「ℵ」(アレフ)と表す。
^ 1. イラストはかわいいフリー素材集 いらすとや(みふねたかしさん)より。
^ 2. 集合論や計算機科学等においては自然数に 0 を含める方が普通である。本稿ではそれに従うが、自然数から 0 を除く定義を採用しても特に問題は無い。