ここにもう1枚コインを追加して4枚にすると、当然その分「重くなった」と感じる。 （下図）
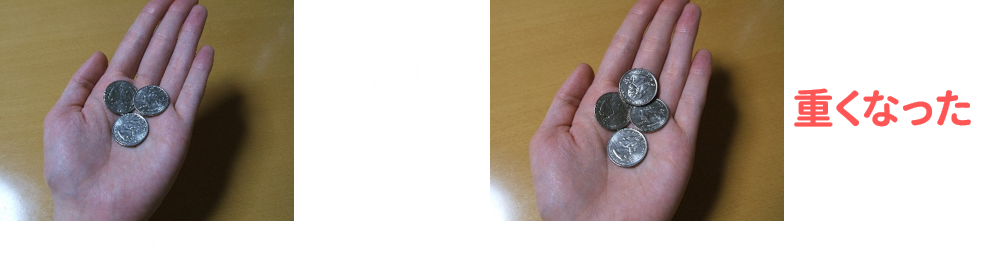
感覚年齢計算スクリプトを用意しました。
高校2年のある日、ホームルームで担任が呟いた。
「年を経るごとに時間が短く感じられるなあ……」
そこで、「実際に流れている時間」と「人間の感じる時間」との関係を定量的に表せないか、と思って考えたのが「年齢対数則」である。
年齢対数則は、 時間が経つのは、実年齢に比例して速くなるように感じられる。 という法則である。言い換えると、 物心付いてから今までに生きた（感覚の上での）時間は、実年齢の対数に比例する。 とも言える。
筆者は「年齢対数則」と呼んでいるが、この法則には「ジャネの法則」という大層な名前が付いているらしい。
また、ざっと検索しても同じような記事がたくさん出てくるので、どうやらみんな似たようなことを考えるているようだ。 〈2013年5月追記〉
掌の上にコインを3枚乗せているとする。
ここにもう1枚コインを追加して4枚にすると、当然その分「重くなった」と感じる。 （下図）
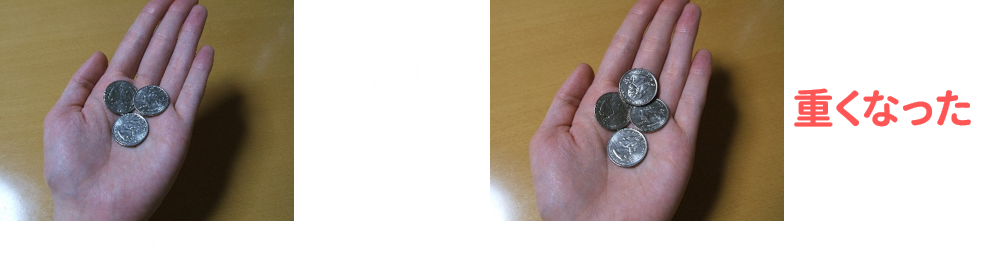
今度は最初のコインの数を15枚にしてみる。
ここにもう1枚コインを追加して16枚にしたら、どう感じるだろうか？
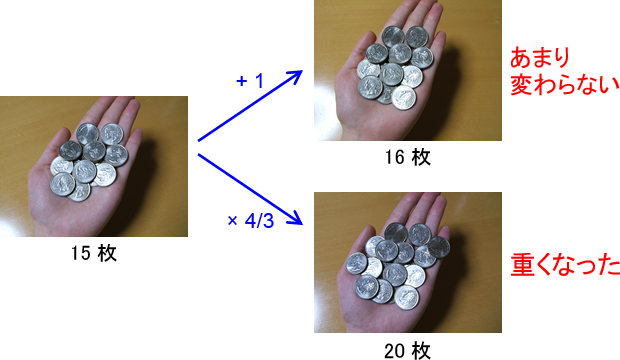
同じ1枚分の変化である筈なのに、3枚から4枚に増えたときと比べると「大した変化ではない」ように感じられる。
では、先程と同程度の変化を感じるにはどうしたら良いだろうか？
元々の枚数が5倍になったのだから、追加する枚数も5倍にしなければ「同じ変化」は感じられないのである。 （下図）
今、最初に x 枚のコインが掌に乗っているとする。
ここに Δx 枚コインを追加したときに感じる重さの変化量を Δy とすると、Δy は Δx に比例し x に反比例する。
この比例係数を α とすると、関係式は
となる。
（このコインの例はあくまで説明用の例として挙げたものであり、実際にはコインの重さでは変化はあまりよくわからない。）
一般に、刺激量 x の刺激を受けているとき、更に Δx だけ刺激を増やしたときに感じる感覚量の変化 Δy は
と表される。この両辺を積分すると、刺激量 x と感覚量 y の関係式
が得られる（β は積分定数）。
つまり、感覚量 y は刺激量 x の対数に比例するのである。
これは「ウェーバーの対数則」（ウェーバー・フェヒナーの法則）などと呼ばれるものである。
実際、人間の感覚に絡む値は対数で表されているものが多い。例えば、
などがそうである。
この「対数則」が年齢にも応用できるのではないか？ と思って考えたのが、本稿の主題である「年齢対数則」である。
同じ「1年」という時間であっても、5歳児にとっての「1年」と、50歳の人にとっての「1年」とでは重みは異なる。
まだ5年しか生きていない子供にとっては、「1年」というのはそれまでの人生の 1/5 を占める長い長い時間である。
一方既に50年を生きた大人にとっては、「1年」というのはそれまでの人生の 1/50 に過ぎない。
ということは、時間の長さの感覚は年齢に反比例する（時間の過ぎる速さは年齢に比例する）と考えることができそうである。
詳しく書くと、以下のようになる。
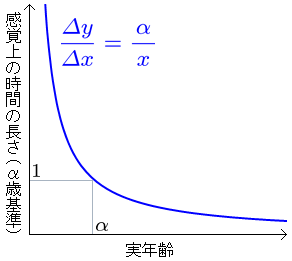
以降、時間感覚の基準を α 歳とする（すなわち α 歳の人にとっての1年を感覚上の「1年」と定める）。
実時間 Δx 年間の、x 歳の人にとっての感覚上の長さ Δy は、α 歳の人にとっては α Δx / x 年間に相当する。
左上のグラフは、各年齢の人の「実時間当たりの感覚上の時間の長さ」Δy / Δx を示したグラフである。
これを x = a から x = b まで積分すれば、人が a 歳から b 歳までに経験する感覚上の時間の累計が求まる。
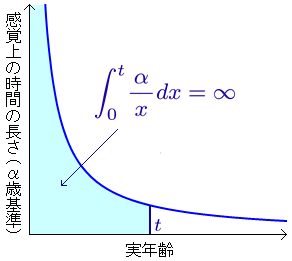
しかし、生まれた瞬間（0歳）からある年齢 t 歳までの感覚上の時間を求めようとして
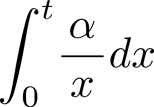
を計算すると、これは ∞ に発散してしまい値が求まらない。
よって、何らかの適当な補正を行うことが必要である。
実際問題としては、0歳児には時間の感覚は無いと考えられる。
そこで、時間の感覚が芽生える年齢を t0 歳とし、それ以降についてのみ考えるものとする。
（この t0 歳というのは3.5歳ぐらいを想定している）[注1]
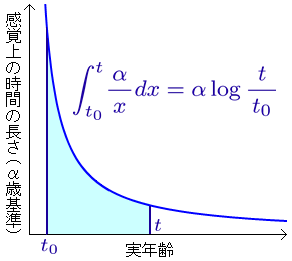
そこで、t0 歳から t (> t0) 歳までの感覚上の時間を求めると、
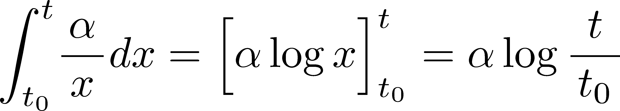
となる。[注2]
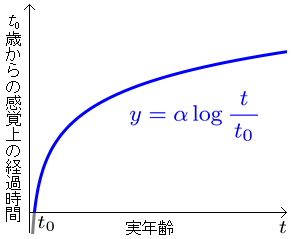
その感覚上の時間を表したのが左上のグラフである。
さて、では時間感覚の上での「人生の折り返し地点」はどこだろうか？
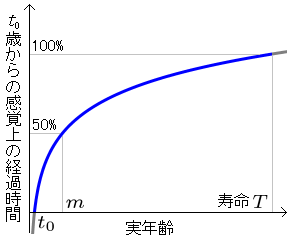
寿命が尽きる年齢を T 歳として、その時点までの一生涯の感覚上の時間を 100% とする。
すると、感覚上の時間が 50% に達する年齢 m が「人生の折り返し地点」であると考えられる。
では、この m とは一体何歳なのだろうか？
より
が得られる。
左上のグラフに見えるように、折り返し地点 m は寿命 T に比べて随分と若い年齢である。
では、具体的な数値を代入して m の値を求めてみよう。
と仮定すると、時間感覚上の「人生の折り返し地点」は
となる（ここで用いた t0 や T の値の妥当性は知らないが、ここを変えても概ね似たような結論が出る）。
よって、時間感覚の上では 10代後半の時点でもう生涯の半分を過ごしてしまっている ということである。
上では t0 = 3.5, T = 83.0 として「人生の折り返し地点」を求めたが、色々な値を代入して計算できるように感覚年齢計算スクリプトを用意した。
勿論、時間感覚は年齢のみならず様々な要因に左右されるものである（例えば、楽しい時間は早く過ぎ、苦痛な時間は長く感じられる）。
この「年齢対数則」もあくまで一つのネタとして、今後の人生を楽しむ上での参考にして欲しい。