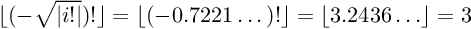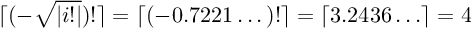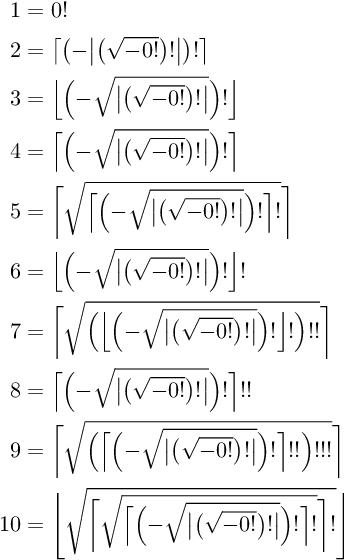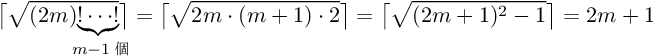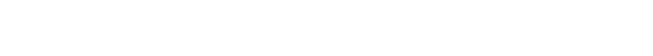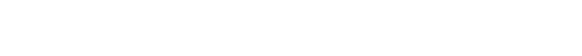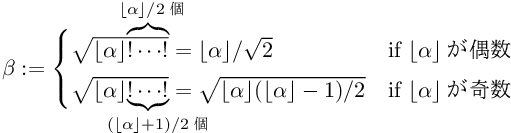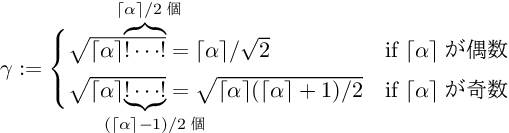「1つの0」問題
4つの4 (four fours) という有名なパズルがある。
これは、数字の 4 を4つ使って色々な数を表そう、という問題である。
では、これが「4つの4」ではなく「4つの0」だったら、或いは「1つの0」だったらどうなるのだろうか?
概要
「4つの4」とは?
「4つの4」とは、
数字の 4 を4つと四則演算を使って色々な数を作れ
という問題である。例えば 0, 1, …, 10 に対しては次のような解がある。
0 = 4 + 4 − 4 − 4
1 = 4 × 4 ÷ 4 ÷ 4
2 = 4 ÷ 4 + 4 ÷ 4
3 = (4 + 4 + 4) ÷ 4
4 = 4 + (4 − 4) × 4
5 = (4 × 4 + 4) ÷ 4
6 = 4 + (4 + 4) ÷ 4
7 = 4 + 4 − 4 ÷ 4
8 = 4 + 4 + 4 − 4
9 = 4 + 4 + 4 ÷ 4
10 = (44 − 4) ÷ 4
この問題については「妖精現実 フェアリアル」さん等に詳しく書かれている。
「4つの0」の話
この「4つの4」に関連して、Twitter で次のようなツイートを見つけた。
【数学】
下に記す四つの整数をつかって、10を作りなさい。ただし、四則演算以外も使用していいとする。
・0
・0
・0
・0
— ふにゃ帽子っ (@soft_HAT) (現在はツイート削除済)
つまり「4つの 0 で 10 を作れ」という問題である。
勿論使える数字が 0 しか無いので四則演算だけでは足りない訳だが、他の演算を幾つか加えることで
10 = ((0! + 0! + 0!)! − 0!)!!! (; 階乗と三重階乗を使用)
などといった解を得ることができる。
そうすると湧いてくるのが、「実は 0 を4つも使う必要は無いのではないか?」という疑問である。そこで、
数字の 0 を1つだけ使って色々な数を作ることはできないだろうか?
と思って試してみた。これが今回の「1つの0」問題である。
使用する演算
「1つの0」を解く上で問題となるのが、「どんな演算の使用を許すべきか」である。
今回はたった1つの 0 から始めて色々な数を作るので、当然足し算や掛け算のような2項演算を使うことはできない。
使用できる演算は、単項演算のみである。
ここでは使用する演算は次の表の通りとした。(表中の x は演算の引数を表す)
単項演算にはこれらの他にも例えば三角関数・指数関数・対数関数のような様々なものが存在するが、本稿では(狭義の)文字を含まない記号のみで表記できるものに限ることにした。
(使用する演算を変えると得られる結果も変わってくるので、興味のある人は色々と試してみてほしい)
色々作ってみる
1
1つの 0 を用いて 1 を構成するのは容易い。
0 の階乗 0! は 1 だからである。
0! = 1
2, 3, 4
1 の次は 2 であるが、2 を構成するのは一筋縄ではいかない。
実数の範囲で数を弄っていても、0 と ±1 ぐらいしか作れない。先へ進むには
一旦虚数を構成し、その階乗(ガンマ関数)を取る
という操作が必要となる。
そこで、虚数単位 i = −1 の階乗 i ! を考えると、その絶対値は次のようになる。
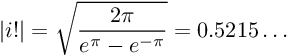
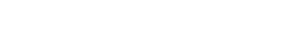 あとは実数の範囲内の操作だけで十分である。
あとは実数の範囲内の操作だけで十分である。
一般の実数に対し、階乗 y = x ! のグラフは下図のようになる。(負整数の階乗は定義されない)
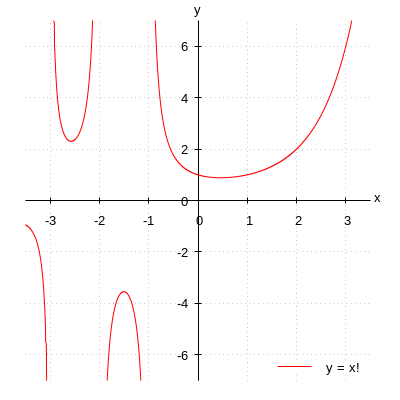
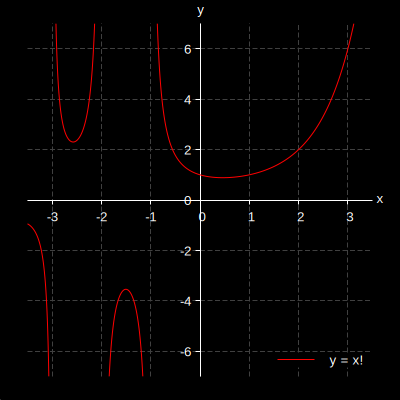 これを利用すると、次のようにして 2, 3, 4 を構成することができる。
これを利用すると、次のようにして 2, 3, 4 を構成することができる。
5, 6, 7, …
2, 3, 4 を構成するに当たっては、自然数以外の値の階乗という得体の知れないものを使ってきた。
しかし、以降の 5, 6, 7, … の探索に耐え得るだけの高精度で一般の階乗の値を計算し続けるのは困難である。
ここからは、既に構成した 2, 3, 4 を元に、階乗は通常の自然数の階乗に限って用いることにする。
探索により発見した 1, 2, …, 10 の構成法を以下に示す。
また、この続きを含めた 1, 2, …, 100 の構成法を別頁に示す。
一般の場合
さて、 1 から 100 までの自然数は構成できることが確認できた訳だが、一般の自然数についてはどうだろうか?
実は、態々探索をせずとも、一般の自然数を構成することが可能である。
これは、以下の2つの補題より示される。
〔補題1〕偶数 2m が構成可能ならば奇数 2m + 1 も構成可能
偶数 2, 4 が構成可能であることは上で確認した通り。
m ≥ 2 のとき、次のようにして 2m を用いて 2m + 1 を構成できる。
〔補題2〕偶数 2m が構成可能ならば偶数 2m + 2 も構成可能
偶数 2, 4, 6, 8, 10 が構成可能であることは上で確認した通り。
m ≥ 5 のとき、2m を用いて 2m + 2 を構成できることを示す。
まず、値 α を次のように構成する。
これを用いて、値 β, γ を次のように構成する。
すると、いずれの場合も β ≤ (2m + 2)2 − 4 ≤ γ かつ γ − β < 2 が成り立つ。
よって、⌈(2m + 2)2 − 4⌉ は ⌈β⌉, ⌊γ⌋, ⌈γ⌉ のいずれかに等しい。従ってこれは構成可能である。
更に、⌈(2m + 2)2 − 4⌉ は 2m + 2 に等しい。従って 2m + 2 は構成可能である。
ところで
以上で「1つの0」と以下の演算から任意の自然数を構成できることが示せた訳であるが、1つ気になる点がある。
それは、「多重階乗」の名のもとに実質的に無限種類の演算を許してしまっている点である。
多重階乗を使用しなくても一般の自然数が構成できるのか否かは現時点で筆者は知らないが、興味がある人は試してみてほしい。
(少なくとも 1, 2, …, 100 は構成できることは別頁に記載の通り確認した)

 = x × (x − k) × (x − 2k) × … × (k 以下の数)
= x × (x − k) × (x − 2k) × … × (k 以下の数)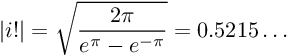

 これを利用すると、次のようにして
これを利用すると、次のようにして