高1の時に数学で出された問題
100! の十進数で表したとき、‘0’ を除いた最も下の桁の数字は何か?
について、「どうせだから 100! を求めてしまおう!」と思って JavaScript でプログラムを書いてみました。 実行する
/* 宣言 */
var LENGTH = 13; // 十分に大きい定数
var MAX_ELEM = 10000000000000; // 各 a[i] の最大値(100を掛けても情報落ちしない程度の桁数)
var a = new Array(LENGTH);
/* 初期化 */
a[0] = 1;
for (i = 1; i < LENGTH; i++) a[i] = 0;
/* n = 1, 2, ..., 100 を順に掛けて表示 */
for (n = 1; n <= 100; n++){
var carry = 0; // 繰り上がり
for (i = 0; i < LENGTH; i++){
a[i] = a[i] * n + carry; // n を掛けて繰り上がりを加える
carry = Math.floor(a[i] / MAX_ELEM); // 次の桁への繰り上がり
a[i] = a[i] % MAX_ELEM;
}
/* 表示 */
for (i = LENGTH - 1; a[i] == 0; i--); // a[i] == 0 なる上位の桁は無視
var result = a[i--].toFixed(0); // toFixed(0) で確実に整数表示にする
for (; i >= 0; i--) result += (a[i] + MAX_ELEM).toFixed(0).substring(1);
document.write(n + "! = " + result + "<br>\n");
}
基本的には、1 × 2 × … × 100 と、順々に掛けていけば 100! は求まります。
しかし、JavaScript では整数は 9,007,199,254,740,992 (= 253) までしか正しく扱うことができません。
それを超えると、精度が落ちてしまいます。
(これは JavaScript で用いられている「倍精度浮動小数点数」という数の表現方法による制約です)
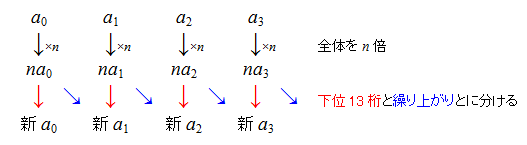
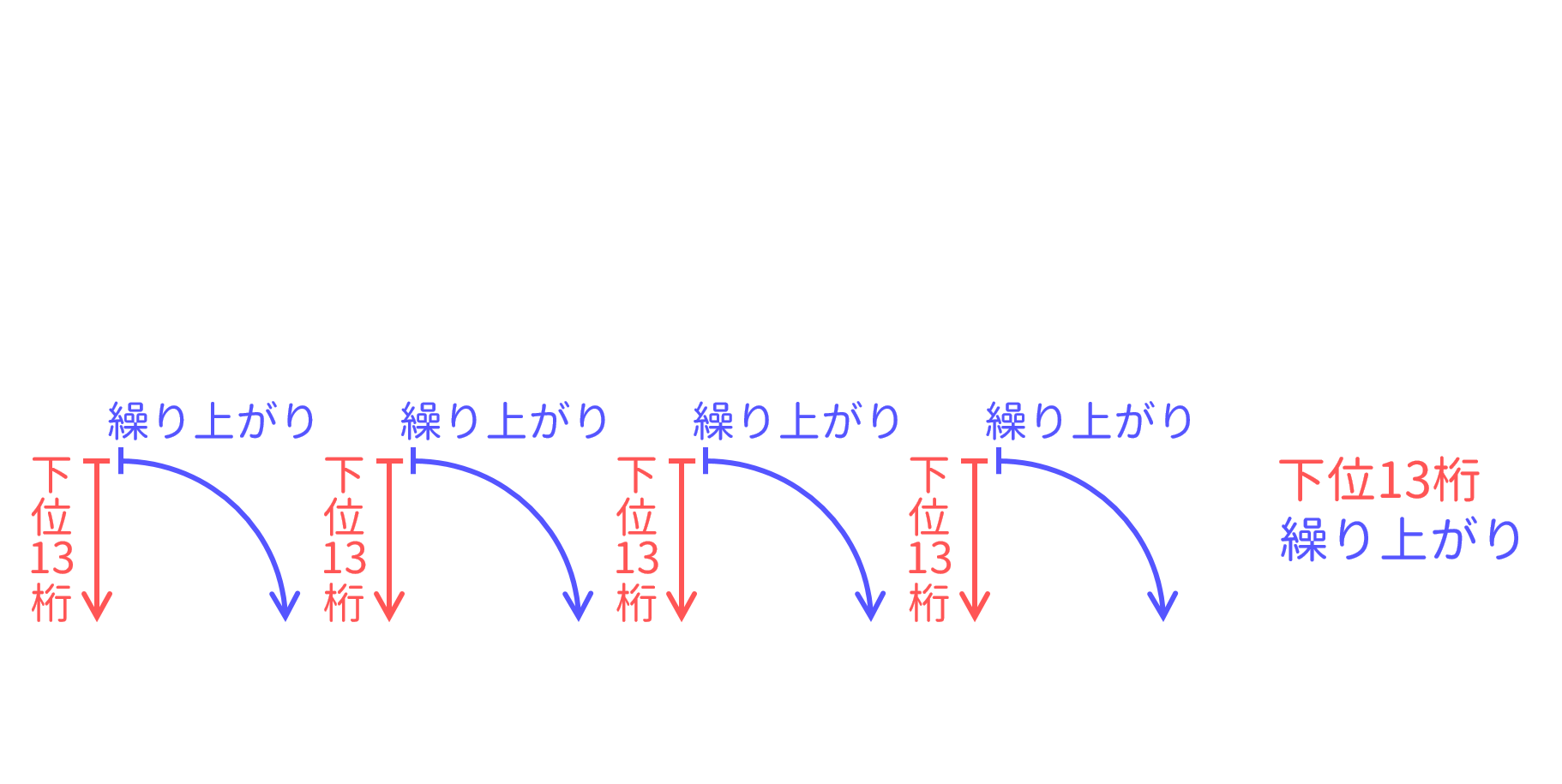
そこで、数値を下の位から13桁毎に a0, a1, a2, … と区切って保持することで、この問題を解決しています(ある種の多倍長整数)。
掛け算をする際は、まず掛ける数 n (= 1, 2, 3, …, 100) を全ての ai それぞれに掛け、それから繰り上がりを処理して13桁毎の区切りを直しています。
区切りを13桁毎にしているのは、このような計算をしても各 ai が 9,007,199,254,740,992 を超えないようにするためです。
因みに、プログラミング言語・処理系によっては、何も考えずとも勝手に多倍長整数(無限精度)で計算してくれるものもあります(Scheme など)。
冒頭の問題ですが、態々プログラムを組んで 100! の値を求めなくても、普通に計算すれば答えはわかります。
100! を素因数分解すると
となることから、100! は 10 (= 2 × 5) の 24 乗では割り切れるが 25 乗では割り切れないことがわかります。
よって、100! ÷ 1024 の1の位を求めればよいと言えます。
数 a と b の1の位の数字が等しいことを「a ≡ b」と表すことにすると
となるので、結局求めるべき数字は 4 です。